Home > Tips > Password Recovery
Password Recovery - Cracking of Secret keys
Cryptanalysis has long relied on the lengthy, patient applications of trail and error in order to crack a code. The advent of electronic computing both hardware means high processor speed, high memory and software means multi tasking, multi processing software platform dramatically enhanced that process. A practical result today is that anyone with a workstation can crack chipertext encrypted with a short key. for example many commercial application like Microsoft Excel (MS Excel) Spreadsheet or Word Processor like Microsoft Word (MS Word) provide password protection for their documents, using encryption to provide the protection and password as they key. If user or creator of the document forget the password he or she cannot open the saved file. We can find so many utility programs to recover the passwords. often using Brute - Force technique.
Many commercial utility program you found in internet they are charging around 50$ to 500$ for finding password. You can download the Visual Basic 6 (VB6) and Visual Basic .Net (VB.Net) complete source code and executable files which is absolutely free and tested. I am not claiming any copyright and responsibility for my programs, you may use complete or part of the solution as you want.
Brute force technique is very simple and efficient, basically it try out all possible combination of password by given character set. The developer of such program admitted that the software includes artificial delays to make the cracking appear to take longer than it really does. because some commercial application have restricted by numbers of attempt for password guising and automatically lock the system for preventing hack.
Brute force cracking works by trying all possible values for the key until the right one is found. Once it succeeds, the attacker can read the message that was encrypted with that key. along with other messages encrypted with that key. the principle defense against brute force cracking is to produce as long a list of legal keys as possible, As the list gets longer, so does the amount of work it could take to guess the right key.
Key Combination of Brute Force Cracking
you can easily calculate numbers of try need to crack down a password if you know the length of password and character set used to make the password.
For example if password length is 3 and for making the password only "a", "b", "c" are used, than possible passwords would be
|
1. |
abc |
|
2. |
acb |
|
3. |
bac |
|
4. |
bca |
|
5. |
cba |
|
6. |
cab |
So you have to try 6 different password to crack the
password, now if password length is 3 and for making the
password only "a","b","c","1"
are used it takes 24 different combination to crack the
password. So now you understand as numbers of character
combination are used to make it is hard to find the
password, it also very much depend on password length, you
can easily find it by using Permutation mathematical
formula.
What is Permutation?
It Returns the number of permutations for a given number of
objects that can be selected from number objects. A
permutation is any set or subset of objects or events where
internal order is significant. Permutations are different
from combinations, for which the internal order is not
significant.
Syntax
PERMUT(number,number_chosen)
Number is an integer that describes the number
of objects.
Number_chosen is an integer that describes the
number of objects in each permutation.
NOTE
-
Both arguments are truncated to integers.
-
If number or number_chosen is nonnumeric,
PERMUT returns the #VALUE! error value.
-
If number ≤ 0 or if number_chosen
< 0, PERMUT returns the #NUM! error value.
-
If number < number_chosen, PERMUT
returns the #NUM! error value.
-
The equation for the number of
permutations is:
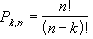
For example PERMUT(3,3) will give output 6,
same way PERMUT(4,3) will give output 24.
If you want to crack or find a 10 byte passwords then depend
on character combination used by making the password, you
need to try this much combination of keys.
|
Sr. |
No of Keys |
Key combination |
|
1 |
3628800 |
Only digits (0-9) |
|
2 |
1.92752E+13 |
Only characters same case
(a-z) |
|
3 |
5.74077E+16 |
Characters with mixed case
(a-z, A-Z) |
|
4 |
9.22393E+14 |
Characters same case and
digits i.e. alphanumeric (a-z, 0-9) |
|
5 |
3.90165E+17 |
Characters with mixed case
and digits (a-z, A-Z, 0-9) |
Home > Tips > Password Recovery